C&R Tree全称是Classification and Regression Tree,即分类及回归树,它是由美国斯坦福大学和加州大学伯克利分校的Breiman等人于1984年提出的,从名称中不难理解,它包含了分类树和回归树,分类树用于目标变量是分类型的,回归树用于目标变量是连续型的。
该算法分割的核心技术取决于目标变量的类型,如果是分类变量,可以选择使用Gini或者是Twoing.如果是连续变量,会自动选择LSD(Least-squared deviation)。
C&R Tree的生长是二叉树, 前面我们讲过的C5.0和CHAID分别是以信息增益率和卡方为标准来选择最佳分组变量和分割点,今天我们讲的C&R Tree,如果目标变量是分类型,则以Gini系数来确认分割点,如果目标变量是数值型,则以方差来确认分割点。
我们先来讲目标变量是分类型的情况,我们称之为分类树:
在C&R Tree算法中,Gini系数反映的是目标变量组间差异程度,系数越小,组间差异越大。Gini系数计算公式如下:
G(t)=1-(t1/T)^2-(t2/T)^2-(t3/T)^2-(tn/T)^2
其中T为总记录数,t1,t2,t3,tn…..分别为输出变量每个类别的记录数
为了比较好理解这个公式,我们以分析结果来理解公式内容,如下图:
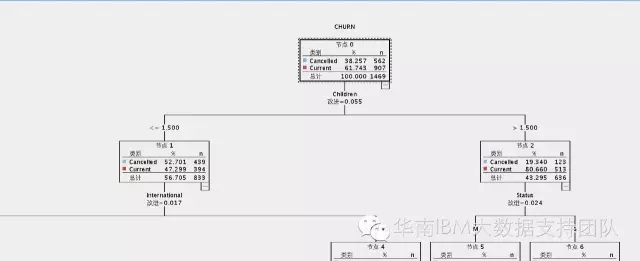
该决策树分析结果,是分析客户的流失为目标,影响的因素有小朋友个数(children),婚姻状态(Status),年龄(age)等,我们先从根节点开始看。
根节点的G(t)=1-(562/1469) ^2-(907/1469)^2=0.472421883
左边节点G(t1)=1-(439/833) ^2-(394/833) ^2=0.498540833
右边节点G(t2)=1-(123/636) ^2-(513/636) ^2=0.311988252
C&R Tree采用Gini系数的减少量来测量异质性下降,因此
ΔG(t)=G(t)-n1/N*G(t1)-n2/N*G(t2)=0.472421883-833/(833+636)* 0.498540833-636/(833+636)* 0.311988252=0.05464854
其中n1是左节点的记录数833,n2是右节点的记录数636,N是根节点的记录数833+636=1469。
计算最终得到的ΔG(t)=0.05464854就是上图中显示的改进=0.055(四舍五入),那么为什么选择这个children<-1.5和children>1/5作为分割点,是因为与其它影响因素相比较,这里计算得到的ΔG(t)最大。所以在整个决策树生长中,可以看到,越往下生长,ΔG(t)越小。
针对连续变量,先对变量按升序排列,然后,从小到大依次以相邻数值的中间值作为将样本分为两组,然后分别计算其ΔG(t)。针对分类变量,由于C&R Tree只能建立二叉树(即只能有两个分支),首先需将多类别合并成两个类别,形成“超类”,然后计算两“超类”下样本输出变量取值的异质性。
在IBM SPSS Modeler中,除了使用Gini系数的减少量作为标准,还可以选择另外两种标准,分别是Twoing(两分法)和Ordered(有序),如下图:
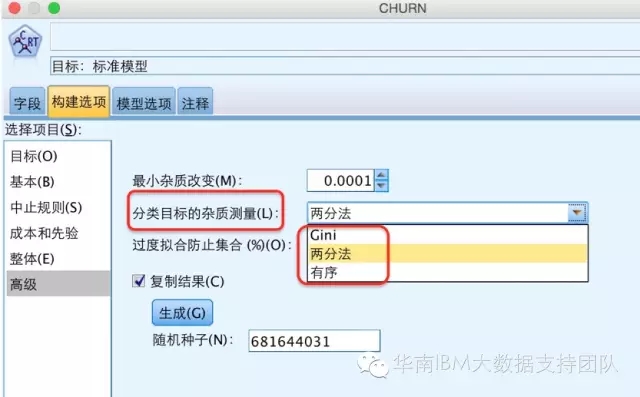
Twoing策略中,输出变量的差异性测度仍采用Gini系数,不同的是,不再以使用Gini系数减少最快为原则,而是要找到使合并形成的左右子节点(两个超类)中分布差异足够大的合并点s,计算公式为:

仍以下图决策树结果为例:
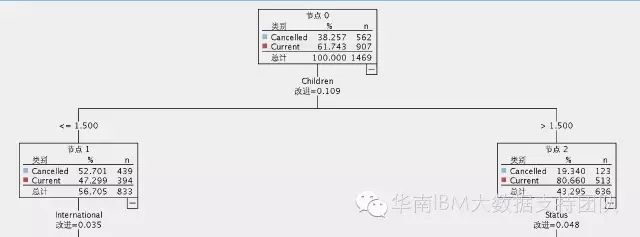

因此

该数值对应着上图第一个根节点的改进=0.109(四舍五入)

可以看到,越是靠近根节点,该值越大。
Order策略适用于有序型输入变量的情况 ,它只限定只有两个连续的类别才可以合并成超类,最终得到最理想的两个超类。
接下来我们来看目标变量是数值型的情况,我们称为回归树。 回归树确定最佳分组变量的策略与分类树相同,主要不同是测试输出变量异质性的指标,
回归树使用的是方差,因此异质性下降的测度指标为方差的减少量,其数学定义为:

其中R(t)和N分别为分组前输出变量的方差和样本量,R(t1),Nt1和R(t2),Nt2分别为分组后左右子树的方差和样本量。使ΔR(t)达到最大的变量应为当前最佳分组变量。我们通过实际例子的结果倒推来理解这个计算公式。
我们使用SPSS Modeler做一个男装销售额(men)预测的场景,因为销售额是数值型,我们选择C&R Tree来实现,那么影响男装销售的输入影响因素有女装销售(women)、电话营销成本(phone)等,得到的决策树分析结果如下:
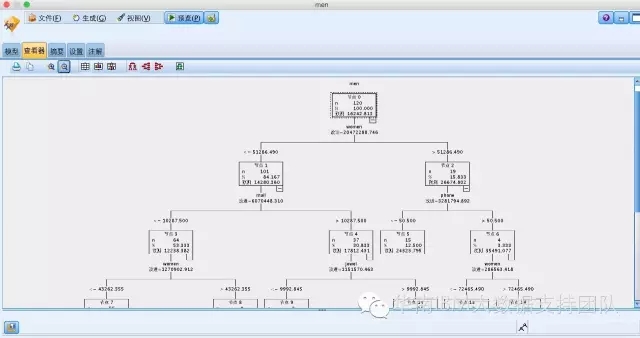
那么为什么生成的决策树会以woman作为最佳分组变量,以51286.490作为分割点呢,因这它计算出来的ΔR(t)最大,大家可以尝试找个例子自己计算看看,这里不再赘述。
最佳分割点的确定方法与最佳分组亦是的确定方法相同。
在IBM SPSSModeler里面,针对 C&R Tree算法,以上介绍的内容是确定分割点的核心标准,对于该算法,还有其它的内容,比如剪枝,交互树建模等,感兴趣的话,可以点击以下链接到官网下载试用!
更多大数据与分析相关行业资讯、解决方案、案例、教程等请点击查看>>>
详情请咨询在线客服!
客服热线:023-66090381

